This article mainly introduces you to the XRD principle and the practice usage of XRD analysis to help you learn XRD from theory to practice.
What Is the XRD Principle?
When a beam of monochromatic X-rays is irradiated on the crystal, the electrons around the atoms in the crystal vibrate under the action of the X-ray periodically changing the electric field, so that each electron becomes a secondary wave source that emits spherical electromagnetic waves. The frequency of the emitted spherical waves corresponds to the incident X-rays.
Based on the periodicity of the crystal structure, the scattered waves of the individual atoms (electrons on the atoms) in the crystal can interfere with each other and superimpose, called coherent scattering or diffraction. The diffraction phenomenon of X-rays in crystals is essentially the result of mutual interference of scattered waves of a large number of atoms. The diffraction pattern produced by each crystal reflects the distribution of atoms inside the crystal.
According to the above XRD principles, the main characteristics of the diffraction pattern of a crystal are two:
1) the distribution law of diffraction lines in space;
2) the intensity of the diffraction beam.
Among them, the distribution law of diffraction lines is determined by the size, shape, and orientation of the unit cell. The intensity of diffraction lines depends on the species of atoms and their positions in the unit cell. Therefore, different crystals have different diffraction patterns.
What Is the Bragg Equation Used in XRD?
The Bragg Equation used in XRD
2dsinθ=nλ
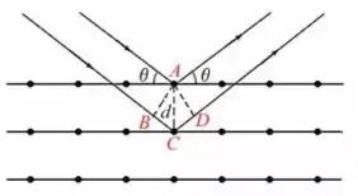
Among them, n is the diffraction order. θ is the angle between the incident ray and the branch ray. θ is half of the diffraction angle, and 2θ is called the diffraction angle.
The Bragg equation reflects the relationship between the direction of the diffraction lines and the crystal structure. For a specific crystal, only the incident ray angle that satisfies the Bragg equation can produce interference enhancement and will show diffraction fringes. This is the fundamental meaning of XRD patterns.
Note: For different crystal systems, there is a definite correspondence between the interplanar spacing d and the unit cell parameters (a, b, c, α, β, γ). After knowing θ and hkl from the XRD spectrum, the Bragg equation can be used. The Bragg equation of XRD can calculate the unit cell parameters.
Scherrer formula using in XRD
Basic principle: When an X-ray is an incident on a small crystal, its diffraction lines will become diffuse and broadened. The smaller the crystal grain, the greater the broadening of the X-ray diffraction band. The Sherrer formula describes the relationship between the grain size and the half-width of the diffraction peak.
The Scherreer formula: D=Kλ/(βcosθ)
The use of this equation to calculate the average grain size requires attention:
1. β is the half-peak width, that is, the width where the diffraction intensity is half of the maximum value, and the unit is expressed in radians.
2. D only represents the grain size in the normal direction of the crystal plane, and has nothing to do with the grain size in other directions.
3. k is the shape factor, k=1.075 for spherical particles, and k=09 for cubic crystals. Generally, k=1 is taken when the requirements are not high.
4. The measurement range is 3~200nm.
Basic principle: Every crystalline substance and its diffraction pattern have a one-to-one correspondence, and it is impossible for two crystals to give the same diffraction pattern.
XRD Phase Analysis
With the improvement of the XRD standard database, XRD phase analysis has become simpler. At present, the most common operation method is to compare the XRD spectrum of the sample with the standard spectrum to determine the phase composition of the sample. The XRD standard database includes JCPDS (ie PDF card), ICSD, CCDC, etc. It is recommended to use the Drawell X-Ray Diffractometer to analyze the XRD spectrum.
In the Drawell X-Ray Diffractometer, you can compare the diffraction pattern of the sample with the standard spectrum, giving the standard spectrum information that matches the measured sample.
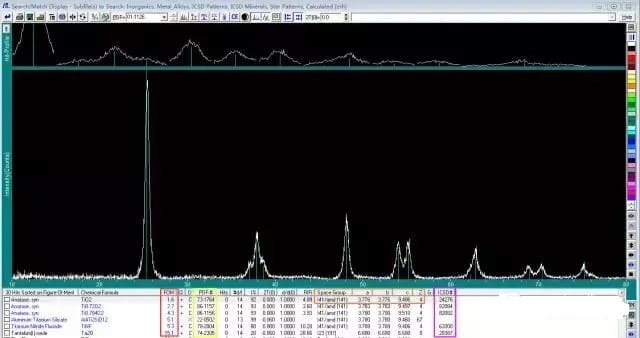
As shown in the figure above, Drawell X-Ray Diffractometer will give the diffraction fringes, phase name, chemical formula, degree of matching (FOM), PDF card number, point group, unit cell parameters, ICSD number, etc. of the standard spectrum.
Among them, FOM is the reciprocal of the matching rate. The smaller the value, the better the matching.
The selected standard material card will pop up the detailed references and diffraction data values of the standard material. The data include the interplanar spacing d, the crystal plane index hkl, and the position and relative intensity of diffraction peaks in the standard spectrum.




